Tournament re-buys are the death of your ROI. No matter how bad the beat you took, no matter how much you think you could win it if you were back in the game, regular resort to re-buys or re-entries—whatever they’re called and however they’re structured—will guarantee most players are losing money.

ITM and mROI

I keep a particular eye on two of my own statistics: in the money  (ITM) rate and median tournament cash ROI (mROI). The first is easy to calculate, it’s just the percentage of times you cash in tournaments: if you’ve cashed in 16 out of 75 tournaments, then your ITM is a very decent 21%. Looking at the top recent tournament players with long records from Carbon Poker, PokerStars, and PartyPoker (as ranked by Official Poker Rankings), their ITM is between 10% and 20%. The top ten players in PokerStars’ $10,300 buy-in event on 18 December had a total of 56,000 games tracked between them; their ITMs were in a very narrow 13% to 17% range, meaning they cashed in every sixth, seventh, or eighth tournament, on the average.

The mROI is a bit more difficult to calculate, because you can’t just keep a tally of wins and cashes, you need to figure the ROI for each cash and keep a list of the ROIs for every game. (My own process is automated.) Now, you could find the mean average by adding all your ROI values and dividing by the number of cashes, but I prefer the median because it prevents the ROI from a big cash from distorting what your usual take is.

I calculate ROI by adding all of my expenses: door fee (in social clubs), buy-ins, re-buys, add-ons, and tips. So say you play a $25 game with a $10 door and an add-on of $10. That’s $45. You win a pot of $200 and pay $20 for a tip. Your cost is $65. The ROI is going to be your profit ($135) divided by the cost, or 208%. If you bubbled the same tournament, got $25, and paid $5 to the dealer (because you’re a nice poker player), your expenses would be $50 and your ROI would be -50%. Simple math.

Once you’ve got a list of ROI values, finding the median is fairly easy. You sort them in numerical order, then look for the value in the middle (if there are an odd number of values) or average values on either side of the middle (if there are an even number of values). In a nine-value sequence:

1  2  3  4  5  6  7  8  9

There are four numbers on either side of “5”, so it’s the middle number and is the median. In a sequence with an even number of values:

0  1  2  3  4   5  6  7  8  9

The “middle” of the sequence is between “4” and “5”, so the median value is the average of those two numbers: 4.5.

So if you have a series of ROI values like this:

327  225  340  53  134  -50  568  43

You sort them into this:

-50  43  53  134  225  327  340  568

And since there are eight values, the median is the average of 134+225, or 180 (rounded up).

How does this tell me anything about re-buys and profitability?

Well, if you’re someone who cashes in one-sixth of the tournaments you play (17% ITM), you need to win enough each time you win to finance the five buy-ins in which you lose, just to stay even.  If your ITM is 13% (winning about one out of eight games) your winnings need to finance the other seven buy-ins. Paying a 10% tip on each win and with a 17% ITM, your mROI needs to be at least 400%; at 13% ITM, break-even mROI increases to 470%. (In casino tournaments where money from the entry fee is held back for paying dealers, the figures are actually higher, because the size of the tip—paid only for wins in social club settings—is smaller in relation to the prize. There the figures would be 500% and 700%, respectively. For most of this discussion I’ll be using the smaller mROI numbers and talking about social clubs unless otherwise mentioned.)

The other thing to keep in mind in this discussion is that these are measures of overall tournament performance. Obviously, if you mostly play smaller games then try your hand at a large tourney and hit big, your overall dollar ROI is going to be great—it’s exactly what I was trying to do with the attempt on the Venetian Deep Stack Main Event last month—it’s just that you can’t count on that happening. The comparison of ITM and mROI provides a gauge of profitability that controls for variations in tournament structures, field sizes, and other factors that change between games and venues.

How well do I have to do?

Let’s start with a player with a respectable ITM of 17%. As explained above, that player needs an mROI of 400% to break even; better to be profitable. That means taking down a prize that’s five times the amount of the combined cost to enter the tournament (plus tip). As we’ll see, that’s difficult enough to to in a large tournament, and almost impossible in a small one.

Example 1. Let’s look at the stats from a recent late-night turbo game with just eight players. Door fee was $10, buy-in was $25, there was one re-buy allowed and no add-on. Three re-buys in the tournament put the prize pool up to $275 and the bubble was paid, so payouts were $175, $75, and $25. Minimum expenditure before tip was $35 (although it would be less if the player spread his door fee costs out over more than one tournament on that day). If the player who won top prize paid an $18 tip, their ROI for the game would be 230%, well below the mROI for a player with 17% ITM. A game that small isn’t profitable unless you’re winning—not just cashing, but winning—more than 25% of the time. If you’ve re-bought, your cost (including tip) is $78, your ROI drops to just 124% and you need to win 40% of these games to break even.

Example 2. Big games have to be no-brainers in terms of profitability, right? The number of players in the field means the top prizes are proportionally larger in relation to the buy-in; and there are more places paid (about one player per starting table or 10% of the field). In this case, we’ll examine a $10,000 Guarantee event with $120 buy-in, one re-buy allowed, and a $50 add-on ($10 door fee). The week we’re looking at the game had 79 entries, 19 re-buys, 54 add-ons, and $14,460 in the prize pool, with payouts as follows:

1. $4,355
2. $3,035
3. $2,165
4. $1,660
5. $1,300
6. $865
7. $575
8. $505

Minimum pre-tip expenditure in this game is $130, but more than two-thirds of the players bought the add-on, so we’ll consider the standard to be $180. Here’s a table comparing ROI for players who pay only the buy-in, the buy-in and add-on, and those who re-buy and add-on (all are considered to tip 10%).

Rank	Prize	Buy-in Only	Buy-in + Add-On	Buy-in + Re-buy + Add-On
1	$4,355	$565 (671%)	$615 (608%)	$735 (493%)
2	$3,095	$433 (601%)	$483 (528%)	$603 (403%)
3	$2,165	$346 (526%)	$396 (447%)	$516 (320%)
4	$1,660	$296 (461%)	$346 (380%)	$466 (256%)
5	$1,300	$260 (400%)	$310 (319%)	$430 (202%)
6	$865	$216 (300%)	$266 (225%)	$386 (124%)
7	$575	$187 (207%)	$237 (143%)	$357 (61%)
8	$505	$180 (181%)	$230 (120%)	$350 (44%)

Even in what is decent-sized field (by Portland standards), just making the money can’t make you profitable. The lowest break-even point for a player with 17% ITM is fifth place in a field of nearly 100 combined buy-ins and re-buys if they don’t do an add-on. With the add-on, it’s third place. The median payout for both of these players is 430% and 328%, respectively (between the 4th- and 5th-place payouts). If the player is cashing in one-sixth of these events with just a buy-in, then they’re statistically likely to be above the break-even point over time. A 17% ITM player with an add-on has to make the top six spots regularly to maintain the 400% mROI.

The re-buying player, on the other hand, can’t afford to just cash one-sixth of the time in events like this. They need to place consistently in the top 3 positions in order for their mROI to maintain at 400% or above.

For players with an ITM of 13%—cashing in one out of eight games—the bar is necessarily higher. The players who don’t re-buy are still in decent shape: a buy-in only player is probably making less money but still profitable if they can make the top 7 payout spots when they cash. A player who gets the add-on needs to place in the top four spots to maintain profitability. But break-even mROI (470%) for a player who regularly re-buys means first place and first place only. Anything less is just throwing money away over the long run.

Example 3. How do the figures pencil out for a casino-style event? For this example, I’ll use the Main Event of the 2011 Venetian Deep Stack Extravaganza IV I played last month.  It was a $2,500 buy-in, with an additional $10 dealer bonus. No re-buys, no add-on. The house got $125 for their take, leaving $2,375 for the prize pool. There were 265 entries, for a total prize pool of $629,375, of which 3% was reserved for dealers and staff and another 0.5% was put into prizes for series point leaders, making the amount awarded to the 27 players who cashed in the tournament a total of more than $607,000. (Just in case you’re wondering, that’s a little under $19,000 for dealers and staff—plus another $2650 in bonus chip money—in a tournament that starts off with 30 tables and runs three days.)

As I mentioned earlier, the mROI needed to play events like these is higher than it is for social gaming clubs. It’s a little counterintuitive, but in casino events you’re paying your rake and something for the dealers (in most instances) as a part of your entry fee. In Portland’s social clubs, only the winners typically pay the dealers, and the size of the tip is  much larger in proportion to the prize money. To break even, what’s left over needs to cover the buy-in costs of future games that are lost, which is why the mROI needed for casino tournaments is greater.

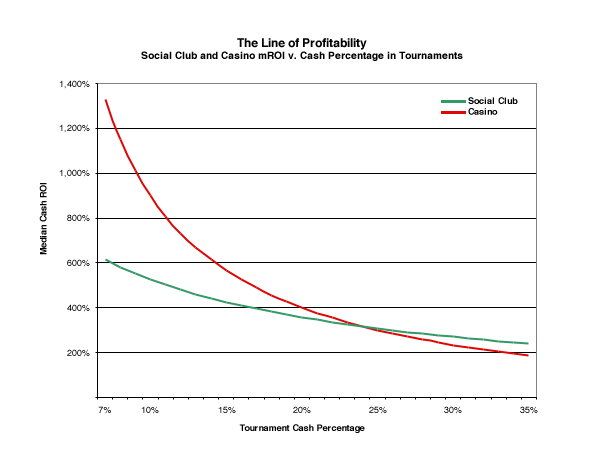
The graphic above shows how the inclusion of a 10% tip into the ROI calculation for a prize affects the profitable mROI value. In the casino prize, the calculation is straightforward: if you win one in six games, your average prize needs to be able to pay for five games in which you lose the buy-in to stay even. If a tip is taken off the top of the prize money, however, all six buy-ins (including the return of the game you win) need to come out of the other 90% of the prize.

Rank(s)	Prize	ROI
1	$145,775	5,708%
2	$89,892	3,481%
3	$60,738	2,320%
4	$43,124	1,618%
5	$33,406	1,231%
6	$27,332	989%
7	$22,777	807%
8	$19,132	662%
9	$15,792	529%
10-12	$12,451	396%
13-15	$9,718	287%
16-18	$7,592	202%
19-27	$6,681	166%

Large events generally pay a smaller percentage of the total prize pool to the winner, but the size of the field inflates the prize pool enough that this tournament—with fewer than three times the number of buy-ins as Example 2 and no add-ons—still has a first prize:buy-in ratio 50% larger. The ROI is nearly 10 times larger (even when Example 2’s tip is ignored, the ROI for a buy-in only player is 3,529%, still significantly under the top ROI for Example 3).

That said, the prizes on the bottom end tend to be flattened out in their structure, with the minimum cashes making money—in this case—just over 2.5 times the buy-in. That flat distribution on the bottom end means the median ROI for cashing in the tournament is just 287%, well short of the 500% needed for profitability with an ITM of 17%. You need to regularly make the last two tables (top 7% of entries) to make games of this size profitable over the long run.

Example 4. An event like the WSOP Main Event has twenty-five times as many entries as something like the DSE Main Event. Pius Heinz’s first prize ROI was a whopping 87,053%. Down on the bottom end, John George in 693rd place (and the other 71 players who got the same amount) had an ROI of just 94%; that’s not enough to cover a single lost buy-in. The median ROI for all players cashing in the 2011 WSOP-ME was 255%; you needed to make it into the top 200 spots (3% of the field) before you were likely to be maintaining the 500% mROI needed for profitability with a 17% ITM (or the top 180 with an ITM of 13%). Events this size are an outlier in the data set, but many of the other WSOP events get several thousand entrants as well, and the payout structure is very similar across the series.

What Does It Mean (Or Median)?

If you play enough tournament poker to have a statistically-significant trail of data, hopefully you’ve been keeping track of how many games you played, what your expenses were, and what you cashed for when you won a prize. Follow these steps to calculate your profitability:

1. Calculate your ITM percentage by dividing your number of cashes by the number of tournaments played then multiply that by 100.
2. For each tournament in which you cashed, calculate the ROI percentage.
• Subtract the total cost of the tournament from the prize money to determine the profit.
• Divide the profit by the total cost of the tournament.
• Multiply by 100.
3. Sort the ROI percentages for your cashes in numerical order, then find the median value (see explanation above). You’ve now found your mROI.

If you’re above the line (depending on the type of games you play) then you’re probably going to be profitable in the long run.

This is a measure of average performance over time; individual circumstances differ. Taking down a first-place prize in a large game is the goal of any tournament poker player, and it doesn’t matter one bit what kind of an ITM Pius Heinz has now that he’s won the WSOP-ME. Getting there is a different story. There’s no way to be a middling, profitable tournament player. Unless you’re exceptional or lucky, you’re probably going to lose. How fast and how much is the question. The re-buy just makes it that much faster.